7# 高等数学的一些复习笔记

# 目录

1. [目录](#目录)

2. [高中遗留物](#高中遗留物)

   1. [因式分解公式](#因式分解公式)

   2. [毕达哥拉斯三角恒等式](#毕达哥拉斯三角恒等式)

   3. [幂简约公式](#幂简约公式)

   4. [反函数](#反函数)

3. [函数](#函数)

   1. [奇偶性](#奇偶性)

      1. [一元函数](#一元函数)

      2. [三角函数](#三角函数)

      3. [复合函数](#复合函数)

      4. [计算法则](#计算法则)

   2. [定义域](#定义域)

   3. [函数单调性](#函数单调性)

   4. [函数凹凸性](#函数凹凸性)

   5. [判断函数间断点](#判断函数间断点)

      1. [二元函数](#二元函数)

   6. [极限](#极限)

      1. [一些极限概念](#一些极限概念)

      2. [极限类型](#极限类型)

      3. [极限做题时的性质](#极限做题时的性质)

      4. [极限计算法则](#极限计算法则)

      5. [近似值](#近似值)

         1. [利用无穷小的性质求函数的极限](#利用无穷小的性质求函数的极限)

      6. [重要极限](#重要极限)

      7. [无穷大小量](#无穷大小量)

         1. [等价无穷大小](#等价无穷大小)

      8. [常用解法](#常用解法)

         1. [抓大头](#抓大头)

      9. [常见的等价变换](#常见的等价变换)

      10. [泰勒展开](#泰勒展开)

         1. [其他型月世界的泰勒展开](#其他型月世界的泰勒展开)

      11. [极限的图形学](#极限的图形学)

      12. [其他型月世界的极限题](#其他型月世界的极限题)

   7. [导数](#导数)

      1. [导数运算法则](#导数运算法则)

      2. [导数公式](#导数公式)

      3. [隐函数求导](#隐函数求导)

         1. [隐函数求导例题](#隐函数求导例题)

      4. [可导导致的连续](#可导导致的连续)

      5. [分离变量](#分离变量)

      6. [原函数](#原函数)

   8. [偏导数](#偏导数)

   9. [积分](#积分)

      1. [凑积分](#凑积分)

      2. [分部积分法](#分部积分法)

      3. [变换积分次序](#变换积分次序)

      4. [不定积分](#不定积分)

      5. [不定积分公式](#不定积分公式)

      6. [经常考的傻逼积分变形](#经常考的傻逼积分变形)

      7. [其他型月世界常见积分](#其他型月世界常见积分)

      8. [定积分](#定积分)

      9. [定积分例题](#定积分例题)

      10. [二重积分](#二重积分)

      11. [变上限积分求导](#变上限积分求导)

      12. [对称限积分](#对称限积分)

      13. [圆相关的积分](#圆相关的积分)

   10. [微分](#微分)

      1. [微分运算法则](#微分运算法则)

      2. [微分方程](#微分方程)

      3. [简易微分方程的求解方法](#简易微分方程的求解方法)

         1. [一阶线性微分](#一阶线性微分)

         2. [一阶线性常微分方程](#一阶线性常微分方程)

         3. [二阶常系数齐次常微分方程 x](#二阶常系数齐次常微分方程-x)

      4. [其他型月世界得求微分通解](#其他型月世界得求微分通解)

      5. [全微分](#全微分)

      6. [微分在近似计算种的应用](#微分在近似计算种的应用)

   11. [级数](#级数)

      1. [级数的敛散](#级数的敛散)

         1. [P 级数](#p-级数)

         2. [交错 P 级数](#交错-p-级数)

         3. [调和级数](#调和级数)

         4. [和函数](#和函数)

      2. [其他型月世界的级数例题](#其他型月世界的级数例题)

4. [各类理论](#各类理论)

   1. [中值定理/均值定理](#中值定理均值定理)

   2. [洛必达](#洛必达)

   3. [条件](#条件)

   4. [牛顿-莱布尼兹 公式](#牛顿-莱布尼兹-公式)

   5. [微分中值定理](#微分中值定理)

      1. [罗尔定理](#罗尔定理)

      2. [拉格朗日中值定理](#拉格朗日中值定理)

      3. [柯西定理](#柯西定理)

   6. [间断点](#间断点)

      1. [第一类间断点](#第一类间断点)

      2. [可去间断点](#可去间断点)

      3. [跳跃间断点](#跳跃间断点)

5. [图形学](#图形学)

   1. [点法式](#点法式)

   2. [二次曲面](#二次曲面)

   3. [直线的表达式](#直线的表达式)

   4. [渐近线](#渐近线)

   5. [向量](#向量)

   6. [模长](#模长)

   7. [方向余弦](#方向余弦)

   8. [方向角](#方向角)

   9. [法向量](#法向量)

      1. [法向量定义](#法向量定义)

      2. [方向向量](#方向向量)

         1. [方向向量定义](#方向向量定义)

      3. [计算与公式](#计算与公式)

      4. [其他型月世界常见的图形题](#其他型月世界常见的图形题)

6. [应用题](#应用题)

   1. [物理应用](#物理应用)

7. [证明题](#证明题)

   1. [中值定理系](#中值定理系)

      1. [拉日型](#拉日型)

      2. [拉日型例题](#拉日型例题)

8. [错题记录](#错题记录)

   1. [我最喜欢的脱裤子放屁题](#我最喜欢的脱裤子放屁题)

# 高中遗留物

- $\ln{A}-\ln{B}=\ln{\frac{A}{B}}$

- $A\ln{B}=-\frac{\ln{B}}{A}$

- $\ln{100}=2\ln{10}$

## 因式分解公式

$\frac{1}{x(C-x)}=\frac{1}{c}[\frac{1}{x}+\frac{1}{C-x}]$

> 理解: 分母拆开看 W±M, 分子上同分之后是 1, x+50-x=50, 提出 50 得证

$\frac{1}{f(x)(g(x))}=\frac{a}{f(x)}-\frac{b}{g(x)}$ 求出 a, b 后转换为 $\frac{1}{w}[\frac{1}{f(x)}-\frac{1}{g(x)}]$

## 毕达哥拉斯三角恒等式

$\sin ^{2}\theta +\cos ^{2}\theta =1 \\$

$\tan ^{2}\theta +1\,=\sec ^{2}\theta \\$

$1\,+\cot ^{2}\theta =\csc ^{2}\theta \\$

## 幂简约公式

$\cos ^{2}\theta=\frac{1}{2}({1+\cos{2\theta}})$

$\sin ^{2}\theta=\frac{1}{2}({1-\cos{2\theta}})$

## 反函数

y=f(x)=w, x=g(y), y=g(x)

> 变形

>

> $a^{-\frac{1}{2}}=\frac{1}{\sqrt{a}}\\e^{\ln{x}}=\ln{e^x}=x\\e^{-\ln{x}}=x^{-1}=\frac{1}{x}$

# 函数

## 奇偶性

### 一元函数

- 一次奇

- 二次偶

- 三次奇

- -1 次奇

- 幂函数无

- 对数函数无

### 三角函数

- sin 奇

- cos 偶

- tan 奇

- cot 奇

- arc sin 奇

- arc cos 无

- arc tan 奇

- arc cot 无

### 复合函数

-

### 计算法则

- 奇+奇=偶

- 偶 ± 偶=偶

- 奇 x 奇=偶

- 奇 x 偶=奇

- 偶 x 偶=偶

## 定义域

取 x 存在的区间

## 函数单调性

若函数求一次导后 y`>0, 则函数单调递增, 反之递减

## 函数凹凸性

若函数求两次导后 y``>0, 为极大值, 则函数凹, 反之凸

## 判断函数间断点

若 x=n 直接带入原式无定义, 则使用极限推导 $\to lim_{x=n}$ 原式

### 二元函数

- 分离变量 $f(x,y)\to f_x=f`(x)=\frac{d}{dx},f_y=f`(y)=\frac{d}{dx}$

- 求极值: 分离变量令二者皆等零, A = f_xx, B = f_xy, C = f_yy, B^2-AC<0,A>0, 则为极小值点, 极值为 $x=\frac{-B}{2A}$, $y=\frac{-C}{2A}$

## 极限

### 一些极限概念

- 驻点: $f`(x)$ 存在, f(x) 在 $x=x_0$ 处取到最大值的点为 f(x) 的驻点

### 极限类型

七种未定式

- $\frac{0}{0}$

- $\frac{\infin}{\infin}$

- $0\times\infin$

> $\rightarrow\frac{\infin}{\frac{1}{0}}\rightarrow\frac{\infin}{\infin}$

- $\infin-\infin$

> 通分, 和差化积

- $\infin^0$

> $e^{0\times\ln\infin}\rightarrow{e^{0\times\infin}}$

- $0^0$

> $e^{0\times\ln0}\rightarrow{e^{0\times\infin}}$

- $1^\infin$

> $e^{\infin\ln{1}}\rightarrow e^{\infin\times0}$

>

> > $x^{f(x)} = 1^∞, 则=e^{f(x)\ln{x}}, 同时 e^{f(x)\ln{x}} = 1^∞$

### 极限做题时的性质

- $要使函数f(x)在x=1处连续, 则有\lim_{x\to{1}}f(x)=f(1)$

- 极限趋近于无穷则没有极限 aka.无穷不是极限 wtf

### 极限计算法则

- 确定未定式类型

> Limit properties − if the limit of f(x), and g(x) exists, then:

- $\lim_{x\to a}(x) = a$

- $\lim_{x\to a}cf(x) = c\lim_{x\to a} f(x)$

- $\lim_{x\to a}(f(x))^c = \lim_{x\to a} f(x)^c$

- $\lim_{x\to a}f(x) ± g(x) = \lim_{x\to a} f(x) ± \lim _{x\to a}g(x)$

- $\lim_{x\to a}f(x) · g(x) = \lim_{x\to a} f(x) · \lim _{x\to a}g(x)$

- $\lim_{x\to a}\frac{f(x)}{g(x)} = \lim_{x\to a} \frac{f(x)}{g(x)} , where \lim_{x\to a}g(x)≠0$

### 近似值

- $\lim_{x\to 0}$ 时

> $1-x=1 \\ \sin x = x \\ \tan x = x \\ e^x = 1+x \\ e^{x^a} = 1+x^a \\ \ln(1+x) = x \\ 1-\cos{x} = \frac{1}{2x^2} = -(\cos{x} -1)$

#### 利用无穷小的性质求函数的极限

> - 性质 1: 有界函数与无穷小的乘积是无穷小

> - 性质 2: 常数与无穷小的乘积是无穷小

> - 性质 3: 有限个无穷小相加、相减及相乘仍旧无穷小

### 重要极限

- $\lim_{x\to{0}}\frac{\sin{x}}{x}=1$

- $\lim_{x\to0}(1-x)^{\frac{a}{-x}}=e^a$

- $\lim_{x\to{\infin}}(1+\frac{1}{x})^{ax}=e^a$

- $\lim_{x\to\infin}(1+\frac{1}{ax})^x=e^\frac{1}{a}$

- $lim_{x\to0} 1-cosx = \frac{x^2}{2}$

- $lim_{x\to0} \sqrt{1-x} = \frac{-x}{2}$

- $lim_{x\to0} \sin{x} - \tan{x} = \frac{-(x^3)}{2}$

- $lim_{x\to0} x\sin\frac{n}{x} = 0, sin$ 为有界函数, x 为无穷小量, 无穷小量 × 有界函数=0

- $lim_{x\to1} \ln{x} = x-1$

### 无穷大小量

> 无穷大小量的阶数: 趋近于无穷大小时, 将原式作为极限计算, 例如:

- $\lim_{x\to 0}\left({x^2}\right) = {x^2}$

- $\lim_{x\to 0}\left({1-\cos{x}}\right) = \frac 1{x^2}$

- $\lim_{x\to 0}\left(\sqrt{1-{x}}-1\right) = -\frac 1{2}{x}$

- $\lim_{x\to 0}\left(\sin{x}-\tan{x}\right) = {x}-\frac 1{2}{x^3}$

#### 等价无穷大小

> $lim_{x\to0} [f(x)/g(x)] = 1$, 即为等价无穷小

### 常用解法

- $sinx \to x | sinAx \to Ax$

#### 抓大头

> 看最高次幂到前面的系数

### 常见的等价变换

> $x\to0$ 时

- $sin(x) \to x$

- $sin^2(x) \to x^2$

- $ln(1+2x) \to 2x$

- $xsinx \to x^2$

- $e^x-1\to{x}$

### 泰勒展开

$

\begin{aligned}

e^{x} &=\sum_{n=0}^{\infin} \frac{1}{n !} x^{n}=1+x+\frac{1}{2 !} x^{2}+\cdots \in(-\infin,+\infin) \\

\sin x &=\sum_{n=0}^{\infin} \frac{(-1)^{n}}{(2 n+1) !} x^{2 n+1}=x-\frac{1}{3 !} x^{3}+\frac{1}{5 !} x^{5}+\cdots, x \in(-\infin,+\infin) \\

\cos x &=\sum_{n=0}^{\infin} \frac{(-1)^{n}}{(2 n) !} x^{2 n}=1-\frac{1}{2 !} x^{2}+\frac{1}{4 !} x^{4}+\cdots, x \in(-\infin,+\infin) \\

\ln(1+x) &=\sum_{n=0}^{\infin} \frac{(-1)^{n}}{n+1} x^{n+1}=x-\frac{1}{2} x^{2}+\frac{1}{3} x^{3}+\cdots, x \in(-1,1] \\

\frac{1}{1-x} &=\sum_{n=0}^{\infin} x^{n}=1+x+x^{2}+x^{3}+\cdots, x \in(-1,1) \\

\frac{1}{1+x} &=\sum_{n=0}^{\infin}(-1)^{n} x^{n}=1-x+x^{2}-x^{3}+\cdots, x \in(-1,1)\\

(1+x)^{\alpha} &=1+\sum_{n=1}^{\infin} \frac{\alpha(\alpha-1) \cdots(\alpha-n+1)}{n !} x^{n}=1+\alpha x+\frac{\alpha(\alpha-1)}{2 !} x^{2}+\cdots, x \in (-1,1)\\

\arcsin x &=\sum_{n=0}^{\infin} \frac{(2 n) !}{4^{n}(n !)^{2}(2 n+1)} x^{2 n+1}=x+\frac{1}{6} x^{3}+\frac{3}{40} x^{5}+\frac{5}{112} x^{7}+\frac{35}{1152} x^{9}+\cdots,x \in (-1,1)\\

\arctan x &=\sum_{n=0}^{\infin} \frac{(-1)^{n}}{2 n+1} x^{2 n+1}=x-\frac{1}{3} x^{3}+\frac{1}{5} x^{5}+\cdots+x \in[-1,1]\\

\tan x &= \sum_{n=1}^{\infin} \frac{B_{2 n}(-4)^{n}\left(1-4^{n}\right)}{(2 n) !} x^{2 n-1}=x+\frac{1}{3} x^{3}+\frac{2}{15} x^{5}+\frac{17}{315} x^{7}+\frac{62}{2835} x^{9}+\frac{1382}{155925} x^{11}+\frac{21844}{6081075} x^{13}+\frac{929569}{638512875} x^{15}+\cdots, x \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)

\end{aligned}

$

#### 其他型月世界的泰勒展开

- $\sqrt{1+x} = {(1+x)}^\frac{1}{2} = 1+\frac{1}{2x}+o{x}$

- $\sqrt{1-x} = {(1-x)}^\frac{1}{2} = 1-\frac{1}{2x}+o{x}$

### 极限的图形学

- 若有一点使极限值 = 函数值, 则函数在该点连续

### 其他型月世界的极限题

- 求极限: $\lim_{x\to{0}}(1±f(x))^{g(x)}\\=\lim_{x\to{0}}(1±f(x))^{f(x)k(x)}\\=e^{\lim_{x\to{0}}k(x)} , g(x)=f(x)k(x)$

- $\lim_{n\to\infin}(\frac{1}{\sqrt{1+n^2}}+...+\frac{1}{\sqrt{n+n^2}})=?$

> 夹逼缩放法:

>

> > $\lim_{n\to\infin}\frac{n}{\sqrt{n+n^2}}≤...≤\lim_n{\to\infin}\frac{1}{\sqrt{1+n^2}}$

> >

> > > 求极限得 1≤...≤1, 即 ...=?=1

- 极限 $lim_{x\to0} {[e^(x^2)]-1}/cosx -1$

> 换元法 $x^2 = u$, 等价 $(e^x)-1\to x$, 变形 $cosx-1 = -(1-cosx), lim_x\to0 1-cosx = \frac{x^2}{2}, -(1-cosx)=\frac{-x^2}{2}$, 带入原极限求得 -2

- $极限 lim_{x=1} x^\frac{1}{x-1}, 原极限为1^∞型, 转换为 e^{\frac{1}{x-1}lnx}\rightarrow lim_{x\to 1}\ln(x), x-1\\带入得 e^{\frac{1}{x-1}x-1}=e, x=1无定义且极限存在, 则x=1为可去间断点$

- 第一判定定理

> 啥我也不知道

- 极值点产生驻点和不可导点, 即函数一阶导=0 或不存在.

## 导数

定义:

> $\lim_{x\to 0} \frac{f(X)-f(x)}{X-x}$

### 导数运算法则

- $(A±B)' = A' ± B'$

- $(AB)' = A'B + AB' 前导后不导+后导前不导$

- $(\frac{A}{B})' = \frac{A'B - AB'}{B^2}$

- $dz=\frac{\partial{z}}{\partial{x}}dx+\frac{\partial{z}}{\partial{y}}dy$ (这个是全微分)

> $z`=\frac{\partial{z}}{\partial{x或者y}}$

- $xy=t,\frac{d^2x}{dy^2}=\frac{dy}{dx}\frac{dt}{dx}$

### 导数公式

$

C`=0, C为常数 \\

x^a`=ax^{a-1} \\

\sqrt{x}`= \frac{1}{2\sqrt{x}} \\

\frac{1}{\sqrt{x}}`=-\frac{1}{2x^{\frac{3}{2}}} \\

a^x`=a^x\ln{a} \\

e^x`=e^x \\

e^{ax}`=ae^{ax} \\

\log_a{x}`=\frac{1}{x}\ln{a} \\

\ln{x}`=\frac{1}{x} \\

\sin{x}`=\cos{x} \\

\sin^2{x}`=\sin{2x} \\

\cos{x}`=-\sin{x} \\

$

- (tan x)' = sec^2 x

- (sec x)' = sec x + tan x

- (cot x)' = -csc^2 x

- (csc x)' = -csc x \* cot x

- $\arcsin{x}`=\frac{1}{\sqrt1-x^2} = -\arccos{x}`$

- $\arctan{x}`=\frac{1}{1+x^2} = -arccot{x}`$

- (1/x)' = -1/x^2

- $\frac{1}{x^2}`=-\frac{2}{x^3}$

- $\ln(1+e^x)' = e^x/(1+e^x)$

- $\ln[f(x)+C]' = \frac{1}{f(x)+C * f'(x)}$

- $[e^{f(x)^n}]' = \frac{e^{{f(x)}^n}}{f(x)^n}'$

- $(e^{\digamma{(x)}})`=[\digamma{(x)}]`e^{\digamma{(x)}}$

- $|f(x)|` = \frac {f(x)}{|f(x)|}$

- $(x^{\sin{x}})`=(e^{\sin{x}\ln{x}})`=(\cos{x}\ln{x}+\frac{\sin{x}}{x})x^{\sin{x}}$

### 隐函数求导

- 把 n 元隐函数看作(n+1)元函数, 通过多元函数的偏导数的商求得 n 元隐函数的导数

- 针对 1 元隐函数, 把 y 看作 x 的函数, 利用链式法则在隐函数等式两边分别对 x 求导, 再通过移项求得${\frac {dy}{dx}}$的值

- 针对 2 元隐函数, 把 y,z 看作 x 的函数, 利用链式法则在隐函数等式两边分别对 x 求导, 令 dz=0, 再通过移项求得${\frac{\partial y}{\partial x}}$的值

#### 隐函数求导例题

- $设函数y=y(x)由方程\ln(x^2+y)=x^3y+\sin x确定, 求\frac{dy}{dx}|x=0$

> $复合函数\ln(w)求导得|\frac{w`}{w}|, 复合函数x^3y求导得3x^2y+x^3y`\\\rightarrow\frac{dy}{dx}=\frac{2x+y`}{x^2+y}=3x^2y+x^3y`+\cos x\\带入x=0得\frac{y`}{y}=1,x=0带入原方程得y=1,则\frac{y`}{1}=1, y`=1, 即\frac{dy}{dx}|{x=0} =1$

### 可导导致的连续

$已知函数Q(x)在点x=0处可导,函数f(x)=W(x)Q(W(x)), 则f`(w)=\frac{f(x)-f(w)}{x-w}$

### 分离变量

> 把原式化为 xdx=ydy

### 原函数

- 可作为共同原函数的函数导数相同.

## 偏导数

> 对谁求导谁是变量, 其他为常数.

## 积分

逆求导=积分

### 凑积分

- 一个函数: $dx=\frac{1}{x}d(ax+b)$

- 复合函数: $y`dx=dy$

### 分部积分法

假设${\displaystyle h(x)\ }$与${\displaystyle k(x)\ }$是两个连续可导函数. 由乘积法则可知

> ${\displaystyle {\frac {{\rm {d}}(hk)}{{\rm {d}}x}}={\frac {{\rm {d}}h}{{\rm {d}}x}}k+h{\frac {{\rm {d}}k}{{\rm {d}}x}}}$

不定积分形式的分部积分方程

> ${\displaystyle \int {\frac {{\rm {d}}h}{{\rm {d}}x}}k\ {\rm {d}}x=hk-\int h{\frac {{\rm {d}}k}{{\rm {d}}x}}\ {\rm {d}}x}$

简化

> $\int u\,dv=uv-\int v\,du$

注意:

- 分布积分 u 的选择遵守优先级原则:

> 反三角函数 > 对数函数 > 幂函数 > 指数函数 > 三角函数 > 常数 > 变量

### 变换积分次序

> 画坐标画积分区间, 然后先交写上线 balabala 从 x 型换成 y 型

### 不定积分

计算最后加常数

### 不定积分公式

$

\int k \mathrm{dx}=kx+C \\

\int x^\mu \mathrm{dx}=\frac1{\mu+1}x^{\mu+1}+C(\mu \ne -1) \\

\int\frac{1}{±x}\mathrm{dx}=±\ln|x| + C \\

\int a^x \mathrm{dx}=\frac{a^x}{\ln a} + C \\

\int e^{±x} \mathrm{dx}=±e^{±x} + C \\

\int \ln x\mathrm{dx}=x\ln x-x + C \\

\int \sin x \mathrm{dx}=-\cos x + C \\

\int \sin ^2x\mathrm{dx}= \frac{1}{2}\left(x-\frac{1}{2}\sin \left(2x\right)\right)+C\\

\int \cos x \mathrm{dx}=\sin x + C \\

\int \cos^2 x \mathrm{dx}=\frac 1{2}(x+\frac 1{2}\sin{2x}) + C \\

\int\sec x\tan x\mathrm{dx}=\sec x + C \\

\int \sec^2 x \mathrm{dx}=\int \frac1{\cos^2 x}\mathrm{dx}=\tan x + C \\

\int \csc x\cot x\mathrm{dx}=-\csc x + C \\

\int \csc^2x\mathrm{dx}=\int \frac1{\sin^2x}\mathrm{dx}=-\cot x + C \\

\int \tan x\mathrm{dx}=-\ln|\cos x| + C \\

\int \cot x \mathrm{dx}=\ln|\sin x| + C \\

\int \sec x \mathrm{dx}=\ln|\sec x+\tan x| + C \\

\int \csc x\mathrm{dx}=\ln|\csc x -\cot x| + C \\

$

### 经常考的傻逼积分变形

$

\int\frac{1}{x^2}\mathrm{dx}=-\frac{1}{x} + C \\

\int\frac{1}{\sqrt{x}}\mathrm{dx}=2\sqrt{x} + C \\

\int \frac{1}{x+1\:}\mathrm{dx}=\ln|x+1|+C \\

\int \frac{\mathrm{dx}}{x^2+a^2}=\frac1{a}\arctan {\frac{x}{a}} + C \\

\int \frac{\mathrm{dx}}{x^2-a^2}=\frac1{2a}\ln|\frac{x-a}{x+a}| + C \\

\int \frac{\mathrm{dx}}{\sqrt{a^2-x^2}}=\arcsin \frac{x}{a} + C \\

\int \frac{\mathrm{dx}}{\sqrt{x^2\pm a^2}}=\ln|x+\sqrt{x^2\pm a^2}| + C \\

\int \sqrt{a^2-x^2}\mathrm{dx}=\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}\arcsin \frac{x}{a} + C \\

\int \sqrt{x^2\pm a^2}\mathrm{dx}=\frac{x}{2}\sqrt{x^2\pm a^2}\pm \frac{a^2}{2}\ln|x+\sqrt{x^2\pm a^2}| + C \\

\int \frac{e^{a\sqrt{x}}}{\sqrt{x}}\mathrm{dx} = \frac{2}{a}{e^{a\sqrt{x}}} + C \\

\int \frac{a}{b-{c{x}}}{dx} = \frac{-a}{c}\ln|{b}-{c}{x}| + C \\

\int \frac{\mathrm{dx}}{\sqrt{1-x^2}}=\arcsin x + C \\

\int \frac{\mathrm{dx}}{1+x^2}=\arctan x + C \\

\int \sin ^2\left(\frac{x}{2}\right)dx=\frac{1}{2}\left(x-\sin \left(x\right)\right)+C\\

\int \cos ^2\left(\frac{x}{2}\right)\mathrm{dx} = \frac 1{2}(x+\sin{x}) + C \\$

### 其他型月世界常见积分

- $曲线积分\int_Lf(x)ds, ds=\sqrt{1+f`(x)^2}dx$

> 先找积分区间 L

>

> > $再找出f(x)的斜率 k=\frac{y_1-y_2}{x_1-x_2}$

> >

> > > $然后套公式y-y_0=k(x-x_0)求出y=?,x=?,\\ds=什么什么dx$

> > >

> > > > $x,y替换到原函数里得到一个新的积分\\\int_{x的区间}x或者f(x)社么什么dx, 然后求积分就完了$

> > > >

> > > > > 一阶导=斜率

### 定积分

> 使用换元法积分区间也要变

### 定积分例题

- $\int_0^1\:(2x+k)dx = 2, k=1$

- $\int_0^1\:\frac{1}{x+1}$

> $令x+1=u, 原函数=\int_{0+1}^{1+1}\:\frac{1}{u}du=\ln|u|_1^2\:=\ln{2}-\ln{1}=\ln{2}-0=\ln{2}$

### 二重积分

- 性质 A: $\int\int_{区间D}dxdy=$ 区间 D 的面积

- 性质 B: $\int\int_{区间D}x dxdy$ 需要画出区间后积分计算

### 变上限积分求导

> 积分上限为参数, 下限为常数, 则 $\frac{d}{dx}\int_0^x{f(t)dt} = F(x)-F(a)=f(x)\times{x`}, f(x)=?$

>

> > 若求 x=? 时的值, 则直接带入 x 到 $f(x)=?$ 中求出值.

### 对称限积分

> 形如 $\int_{-a}^a\:f(x)dx,$ 其中

>

> > 被积函数为偶函数, 则积分可以写作 $2\int_0^a\:f(x)dx$ >> 被积函数为奇函数, 则积分等于 0

### 圆相关的积分

- $x^2+y^2=r^2$ 是圆心在圆点的表达式 , $\int\int_Df(x,y)dxdy$ 的积分可以写成 $\int\int_Dg(r)dO=\int_\theta d\theta\int_rg(r)rdr, \theta\in[0,2\pi],$ O 是极坐标的什么什么概念衍生, 极坐标是用角度和长度描述位置的坐标系

- 格林公式:

> 设闭区域 D 由分段光滑的简单曲线 L 围成，函数 P(x,y) 及 Q(x,y) 在 D 上有一阶连续偏导数, 则有: ${\displaystyle \iint \limits_{D}\left({\frac {\partial Q}{\partial x}}-{\frac {\partial P}{\partial y}}\right)\mathrm {d} x\mathrm {d} y=\oint_{L^{+}}(P\mathrm {d} x+Q\mathrm {d} y)}$

>

> 其中 L+ 是 D 的取正向的边界曲线.

>

> > 简化版: 前后偏分后 $\int\int_D Q(x)-P(x) dxdy=-S_D$

## 微分

> 微分 d(f(x)) = f'(x)dx

### 微分运算法则

- d(A±B) = dA ± dB

- d(A*B) = A*dB + B\*dA

- $d(A/B) = \frac{(B*dA - A*dB)}{B^2}$

- d(C*A) = C*dA

- $dF(g(x))=\frac{F`(g(x))}{g`(x)}$

### 微分方程

以下是常微分方程的一些例子, 其中$u$为未知的函数, 自变量为$x$, $c$及$\omega$ 均为常数.

- 非齐次一阶常系数线性微分方程:

> ${\displaystyle {\frac {du}{dx}}=cu+x^{2}.}$

- 齐次二阶线性微分方程:

> ${\displaystyle {\frac {d^{2}u}{dx^{2}}}-x{\frac {du}{dx}}+u=0.}$

- 描述谐振子的齐次二阶常系数线性微分方程:

> ${\displaystyle {\frac {d^{2}u}{dx^{2}}}+\omega ^{2}u=0.}$

- 非齐次一阶非线性微分方程:

> ${\displaystyle {\frac {du}{dx}}=u^{2}+1.}$

- 描述长度为$L$的单摆的二阶非线性微分方程:

> ${\displaystyle L{\frac {d^{2}u}{dx^{2}}}+g\sin u=0.}$

- 以下是偏微分方程的一些例子, 其中 u 为未知的函数, 自变量为 x

> x 及 t 或者是 x 及 y

- 齐次一阶线性偏微分方程:

> ${\displaystyle {\frac {\partial u}{\partial t}}+t{\frac {\partial u}{\partial x}}=0.}$

- 拉普拉斯方程, 是椭圆型的齐次二阶常系数线性偏微分方程:

> $∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 = 0. {\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=0.}$

- KdV 方程, 是三阶的非线性偏微分方程:

> $∂ u ∂ t = 6 u ∂ u ∂ x − ∂ 3 u ∂ x 3 . {\displaystyle {\frac {\partial u}{\partial t}}=6u{\frac {\partial u}{\partial x}}-{\frac {\partial ^{3}u}{\partial x^{3}}}.}$

### 简易微分方程的求解方法

#### 一阶线性微分

- $形如y`+q(x)y=p(x)的方程$

> $通解公式: e^{-\int p(x)dx}(\int e^{\int p(x)dx}q(x)dx+C)$

#### 一阶线性常微分方程

> 对于一阶线性常微分方程, 常用的方法是常数变易法:

对于方程: ${\displaystyle y'+p(x)y+q(x)=0}$

可知其通解: ${\displaystyle y=C(x)e^{-\int p(x)\,dx}}$

然后将这个通解代回到原式中, 即可求出 C(x)的值

#### 二阶常系数齐次常微分方程 x

> 对于二阶常系数齐次常微分方程, 常用方法是求出其特征方程的解

对于方程: ${\displaystyle y''+py'+qy=f(x)}$

其特征方程: ${\displaystyle r^{2}+pr+q=0}$

根据其特征方程, 判断根的分布情况, 然后得到方程的齐解: ${\displaystyle y_{h}=c_{1}y_{1}+c_{2}y_{2}}$

> 一般的齐解形式为

(在${\displaystyle r_{1}=r_{2}}$的情况下): ${\displaystyle y_{h}=(C_{1}+C_{2}x)e^{rx}}$

(在${\displaystyle r_{1}\neq r_{2}}$的情况下): ${\displaystyle y_{h}=C_{1}e^{r_{1}x}+C_{2}e^{r_{2}x}}$

(在共轭复数根的情况下): ${\displaystyle y_{h}=e^{\alpha x}(C_{1}\cos(\beta x)+C_{2}\sin(\beta x))}$

接者再解特解 yp,可用微分算子计算出 最后,得 y=yh+yp

### 其他型月世界得求微分通解

- 求方程 $2(xy+y)y`=y$ 的通解

> $\begin{aligned}y`=\frac{dy}{dx}&=\frac{y}{2(xy+x)}\\ydx&=2(xy+x)dy\\\frac{y+1}{y}dy&=\frac{1}{2x}dx\\\int\frac{y+1}{y}dy&=\int\frac{1}{2x}dx\\\int 1+\frac{1}{y}dy&=\int\frac{1}{2}\frac{1}{x}dx\\y+\ln{|y|}&=\frac{1}{2}\ln{|x|}+C\\2y+2\ln{|y|}&=\ln{|x|}+C\\e^{2y+2\ln{|y|}}&=e^{\ln{|x|}+\ln{C}}\\e^{2y+\ln^2|y|}&=e^{\ln{|x|}+\ln{C}}\\e^{\frac{1}{\ln{C}}(2y+\ln{|y|^2})}&=e^{\ln{|x|}}\\Ce^{2y}e^{\ln|y|^2}&=x\\由图像知|x|恒>0\\则原方程通解为\\Ce^{2y}y^2&=x\end{aligned}$

- 求方程 $y`+xy^2=0$ 的通解

> $\begin{aligned}y`=\frac{dy}{dx}&=-xy^2\\dy&=-xdxy^2\\\frac{dy}{y^2}&=-xdx\\\int\frac{1}{y^2}dy&=\int-{x}dx\\-\frac{1}{y}&=-\frac{x^2}{2}+\frac{C}{2}\\y&=\frac{2}{x^2+C}\end{aligned}$

- 已知一个解, 求微分方程的常量

> 解导一下然后带入微分方程.

### 全微分

- 公式

> $dz=\frac{\partial{z}}{\partial{x}}dx+\frac{\partial{z}}{\partial{y}}dy$

>

> > 有点则直接带入微分算子求出值, 再带上 dx dy => 值 dx+值 dy

- 设三元的公式

> $f(x,y,z)=balabala, f_x=ba,f_y=la,f_z=bal,dz=-\frac{f_x}{f_z}+-\frac{f_y}{f_z}=\frac{dx}{-dz}+\frac{dy}{-dz}$

### 微分在近似计算种的应用

- $f(x_0+\Delta{x})=f(x_0)+f`(x_0)\Delta{x}$

## 级数

### 级数的敛散

- 条件收敛: 若级数 $∞∑_{n=1} |Un| \to$ 发散, $∞∑n=1 Un \to$ 收敛, 则称级数为条件收敛级数

- 绝对收敛: 若级数 $∞{∑n=1} |Un| \to$ 收敛, 则称级数为绝对收敛级数

- 收敛半径:

> $R=\frac{1}{\rho}=\lim_{n\to\infin}\frac{a_n}{a_{n+1}}, \rho=\lim_{n\to\infin}|\frac{a_{n+1}}{a_n}|, \rho\in{(0,+∞)}$

- 收敛区间:

> 计算收敛半径 R, 然后令含有 x 的 $|f(x)|<R$ 并讨论 x 的范围.

- 收敛域:

> 先求出收敛半径 (-R,R)

>

> > 讨论收敛区间端点的敛散性, 即讨论 x=-R,x=R 时的带入到原级数后的级数的敛散性.

- 交错级数判别敛散性:

> 具有以下形式的级数 ${\displaystyle \sum_{n=0}^{\infin }(-1)^{n}a*{n}\!} \\$ 其中所有的 $a_{n}$ 非负, 被称作交错级数. 如果当 n 趋于无穷时, 数列 $a_{n}$ 的极限存在且等于 0, 并且每个 $a_{n}$ 小于或等于 $a_{n-1}$ (即数列 $a_{n}$ 是单调递减的), 那么级数收敛. 如果 L 是级数的和 ${\displaystyle \sum_{n=0}^{\infin }(-1)^{n}a_{n}=L\!}$ 那么部分和 ${\displaystyle S_{k}=\sum_{n=0}^{k}(-1)^{n}a_{n}\!}$ 逼近 L 有截断误差 ${\displaystyle \left|S_{k}-L\right\vert \leq \left|S_{k}-S_{k-1}\right\vert =a_{k}\!}$

>

> > 简化: $\lim_{n\to\infin}An=0, An≥A{n+1}$, 即单调递减

- 若级数 ${\displaystyle \sum_{n=1}^{\infin }Un\! 收敛, 则\lim_{n\to\infin}Un=0}$

#### P 级数

> 形如 ${\displaystyle\sum_{n=1}^{\infin}} \frac{1}{n^p}$ 其中 n>0 时, p>1 则级数收敛, p<=1 时级数发散

#### 交错 P 级数

> 形如 ${\displaystyle\sum_{n=1}^{\infin}}(-1)^{n-1} \frac{1}{n^p}$ 其中, p>1 时绝对收敛, 0<p≤1 时条件收敛, p≤0 时发散

#### 调和级数

> Harmonic series 是一个发散的无穷级数, 表达式为:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots \,\!}$

#### 和函数

- 一个等比数列的首 n 项之和, 称为等比数列和 (sum of geometric sequence)或几何级数 (geometric series), 记作 $S_{n}$

- 求法

> 求级数收敛域, 再令 S(x)=这个级数=化简化简, 在求导并令 n=0,然后带入求和公式

- 求和公式

> 等比数列 ${\displaystyle S_{n}={\frac {a(1-r^{n})}{1-r}}}$ 等差级数 ${\displaystyle S_{n}={\frac {n}{2}}\,(a+a_{n})\\={\frac {n}{2}}[2a+(n-1)d]\\=an+d\cdot {\frac {n(n-1)}{2}}}$

### 其他型月世界的级数例题

- 设级数 $∞∑_n=1 Bn$ 为正项级数, $∞∑_n=1 (A_n)^2$ 收敛, 则级数 $∞∑_n=1 (-1)^n \frac{|A_n|}{\sqrt{n^2 + B_n}}$

> 绝对收敛.

- 求幂级数 ${\displaystyle\sum_{n=0}^{\infin }\frac{\ln(n+1)}{n}x^{n-1}}$ 的收敛域

> 收敛半径 $R=\frac{1}{\rho},\rho=\lim_{n\to\infin}|\frac{A{n+1}}{A{n}}|, A{n}=\frac{\ln{n+1}}{n}$

>

> > $\begin{aligned}\rho&=\lim_{n\to\infin}|\frac{\frac{\ln(n+1+1)}{n+1}}{\frac{\ln(n+1)}{n}}|\\&=\lim_{n\to\infin}|\frac{\ln(n+1+1)}{n+1}\frac{n}{\ln(n+1)}|\\&=\lim_{n\to\infin}\frac{\ln(n+2)}{\ln(n+1)}\frac{n}{n+1}\\&=\lim_{n\to\infin}|\frac{n+1}{n+2}|\\&=1\end{aligned}\\R=\frac{1}{\rho}=1$ , 原级数收敛区间为(-1,1)

> >

> > > 当 x=-1 时, 原级数= ${\displaystyle\sum_{n=0}^{\infin }\frac{\ln(n+1)}{n}(-1)^{n-1}}$ 为交错级数, 此时判别敛散性\\ $\lim_{n\to\infin}\frac{\ln(n+1)}{n}=\frac{\infin}{\infin}$ =洛 $\frac{f`(x)}{g`(x)}=0$ , 且单调递减, 即 x=-1 时收敛\\当 x=1 时, 原级数= ${\displaystyle\sum_{n=0}^{\infin}\frac{\ln(n+1)}{n}(1)^{n-1}}={\displaystyle\sum_{n=0}^{\infin}\frac{\ln(n+1)}{n}}>{\displaystyle\sum_{n=0}^{\infin }\frac{1}{n}}$ ,即 x=1 时小发散$\rightarrow$ 大发散

> > >

> > > > 综上, 原级数收敛区域为[-1,1)

- $求幂级数\displaystyle\sum_{n=1}^{\infin }\frac{x^n}{3^n}的收敛半径$

> $a_n=\frac{1}{3^n},\frac{a_n+1}{a_n}=\frac{\frac{1}{3^n+1}}{\frac{1}{3^n}}=\frac{3^n+1}{3^n}=\frac{3^n3}{3^n}=3$

# 各类理论

## 中值定理/均值定理

> 給定平面上固定兩端點的可微曲線, 則這曲線在這兩端點間至少有一點, 在這點該曲線的切線的斜率等於兩端點連結起來的直線的斜率

>

> > $假設函數 f 在閉區間 [a,b] 連續且在開區間 (a,b) 可微, 則存在一點 c , a < c < b, 使得 {\displaystyle f'(c)={\frac {f(b)-f(a)}{b-a}}}.$

## 洛必达

洛必达法则可以求出特定函数趋近于某数的极限值, 两函数 f(x),g(x)在以 x=c 为端点的开区间可微 ${\displaystyle c\in {\bar {\mathbb {R} }}}$ 时如果 ${\displaystyle\lim_{x\to c}{f(x)}=\lim_{x\to c}{g(x)}=0} 或 {\displaystyle \lim_{x\to c}{|f(x)|}=\lim_{x\to c}{|g(x)|}=\infin }$ 其中一者成立, 则称欲求的极限 ${\displaystyle\lim_{x\to c}{\frac {f(x)}{g(x)}}}$ 为未定式, 此时洛必达法则表明: ${\displaystyle\lim_{x\to c}{\frac {f(x)}{g(x)}}=\lim_{x\to c}{\frac{f'(x)}{g'(x)}}}$

## 条件

可微代表所有维度下导数存在, 一元下两者等价. 一般情况下, 可微是可导的充分条件[可微一定可导, 可导不一定可微], 可导是连续的充分条件[可导一定连续, 连续不一定可导].

> - 可微=>可导=>连续=>极限存在

> - 一阶偏导数连续=>可微=>一阶偏导数存在

## 牛顿-莱布尼兹 公式

应用条件:

> 要求被积函数在积分区间内连续

一般类型:

> 找 $\int_D$ 上能否存在 x

## 微分中值定理

如果 R 上的函数 f(x) 满足以下条件:(1) 在闭区间 [a,b] 上连续, 在开区间 (a,b) 内可导, 那么:

### 罗尔定理

> - 在开区间 (a,b) 内至少存在一点 ξ ,

> - 当 f(a)=f(b) 时,

> - 使得 f'(ξ)=0

### 拉格朗日中值定理

> - 在开区间 (a,b) 内至少存在一点 ξ ,

> - 使得 $f'(ξ)=\frac{f(b)-f(a)}{b-a}$

### 柯西定理

> 用参数方程表示的曲线上至少有一点, 它的切线平行于两端点所在的弦.

## 间断点

定义:

> 如果函数 f 在点 x 连续, 则称 x 是函数 f 的连续点；如果函数 f 在点 x 不连续, 则称 x 是函数 f 的间断点

### 第一类间断点

定义:

> 给定一个函数 f(x) 如果 $x_0$ 是函数 f(x) 的间断点, 并且 f(x) 在 $x_0$ 处的左极限和右极限均存在的点称为第一类间断点.

### 可去间断点

定义:

> 若 f(x) 在 $x_0$ 处得到左、右极限均存在且相等的间断点, 称为可去间断点. 需要注意的是, 可去间断点需满足 f(x) 在 $x_0$ 处无定义, 或在 $x_0$ 处有定义但不等于函数 f(x) 在 $x_0$ 的左右极限.

>

> > 例如 $f\left({x}\right)={x}^{\frac{1}{x-1}}$ x=1 是 f(x)的可去间断点: 取极限 $\lim_{x\to 1}{x}^{\frac{1}{x-1}}=e^{\frac {x-1}{x-1}}=e$ 得极限存在, 而 x=1 方程无定义, 故为可去间断点.

### 跳跃间断点

定义:

> 设函数 f(x) 在 U($x_0$) 内有定义, $x_0$ 是函数 f(x) 的间断点 (使函数不连续的点), 那么如果左极限 f(x-) 与右极限 f(x+) 都存在, 但 f(x-)≠f(x+), 则称 $x_0$ 为 f(x) 的跳跃间断点, 它属于第一间断点.

# 图形学

## 点法式

$A\left(x-x_{0}\right)+B\left(y-y_{0}\right)+C\left(z-z_{0}\right)=0$

## 二次曲面

| 未退化的一般实二次曲面 | 表达式 | 图像 |

| :-: | :-: | :-: |

| 椭球面 | ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1$ |  |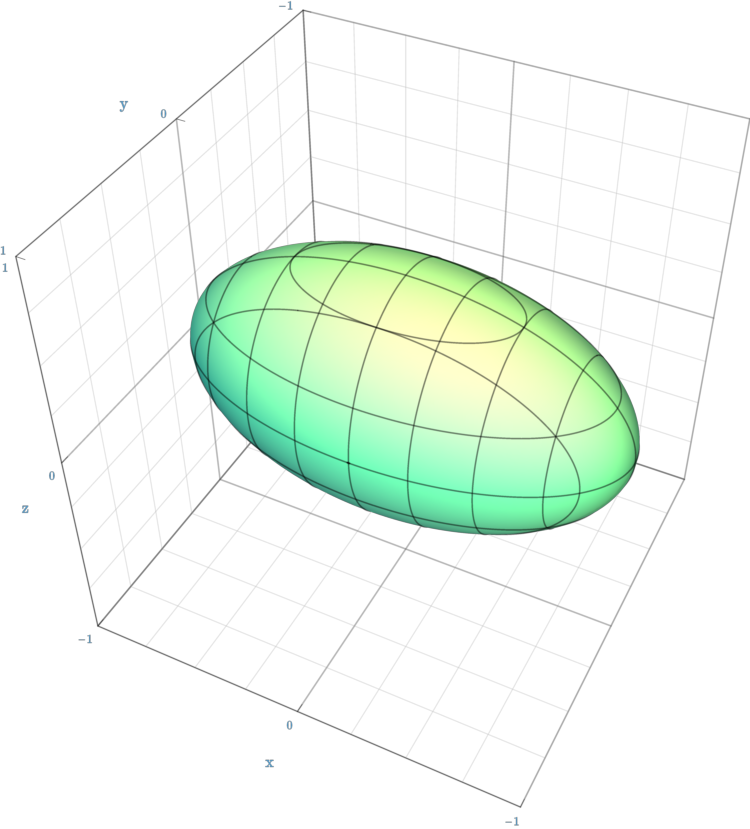

| 椭圆抛物面 | ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-z=0\,$ |  |

| 双曲抛物面 | ${x^{2} \over a^{2}}-{y^{2} \over b^{2}}-z=0\,$ |  |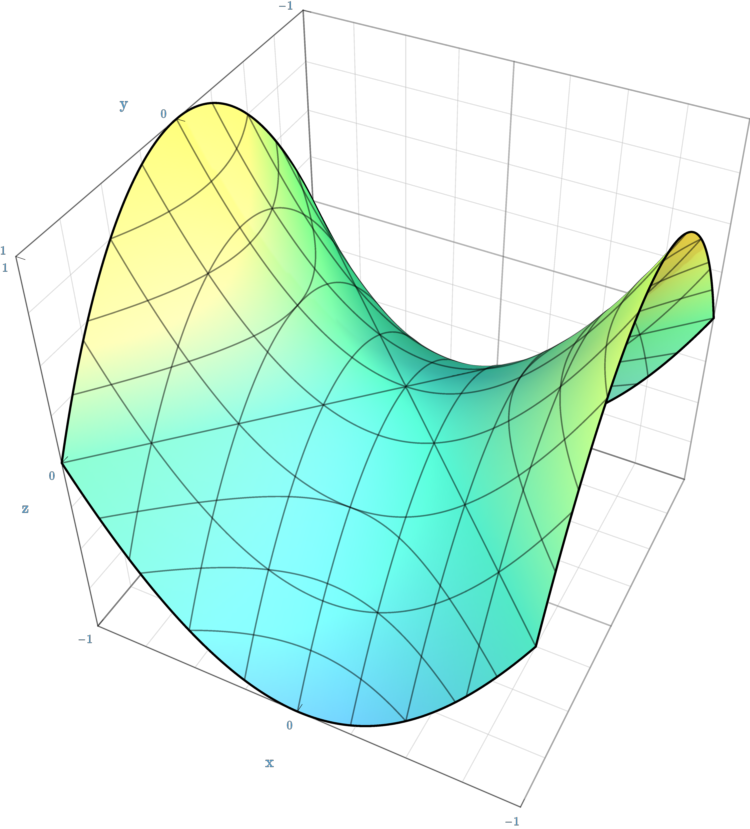

| 单页双曲面 | ${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1\,}$ |  |

| 双叶双曲面 | ${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1\,}$ |  |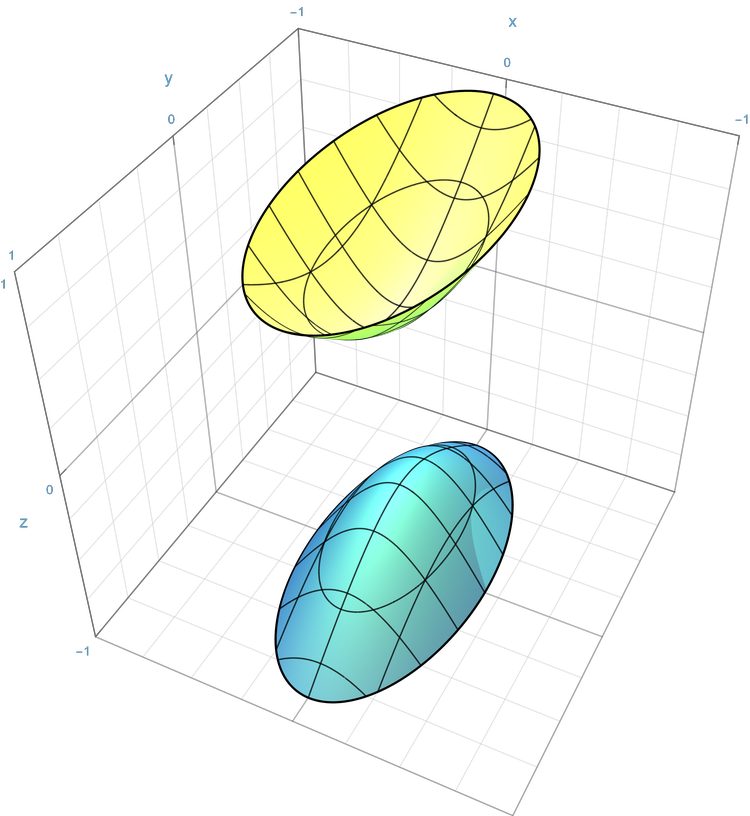

| 特殊二次曲面 | 表达式 | 图像 |

| :-: | :-: | :-: |

| 类球面（一种特殊的椭球面） | ${x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over b^{2}}=1\,$ |  |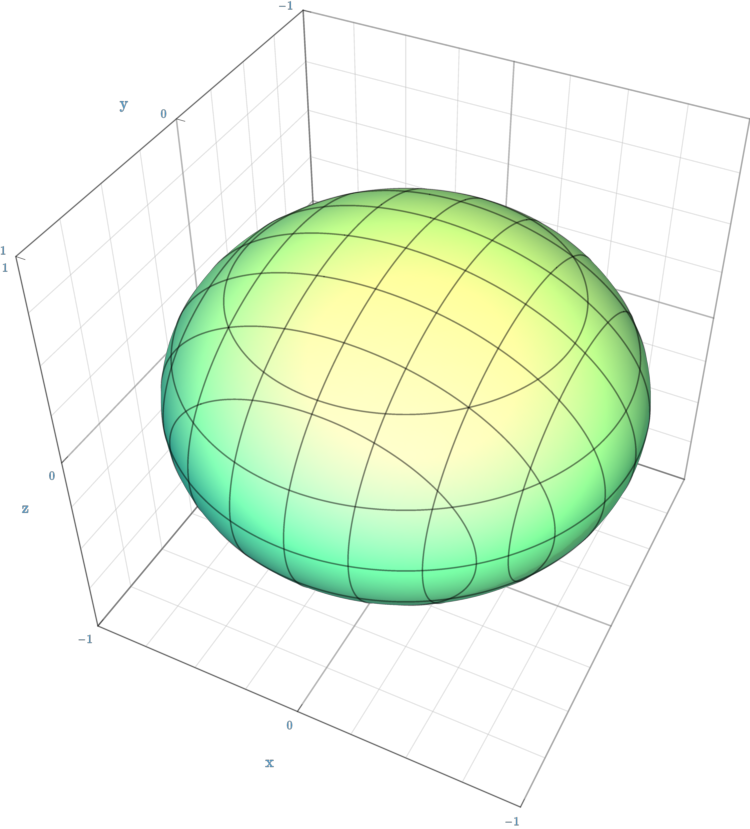

| 球面 | ${x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over a^{2}}=1\,$ |  |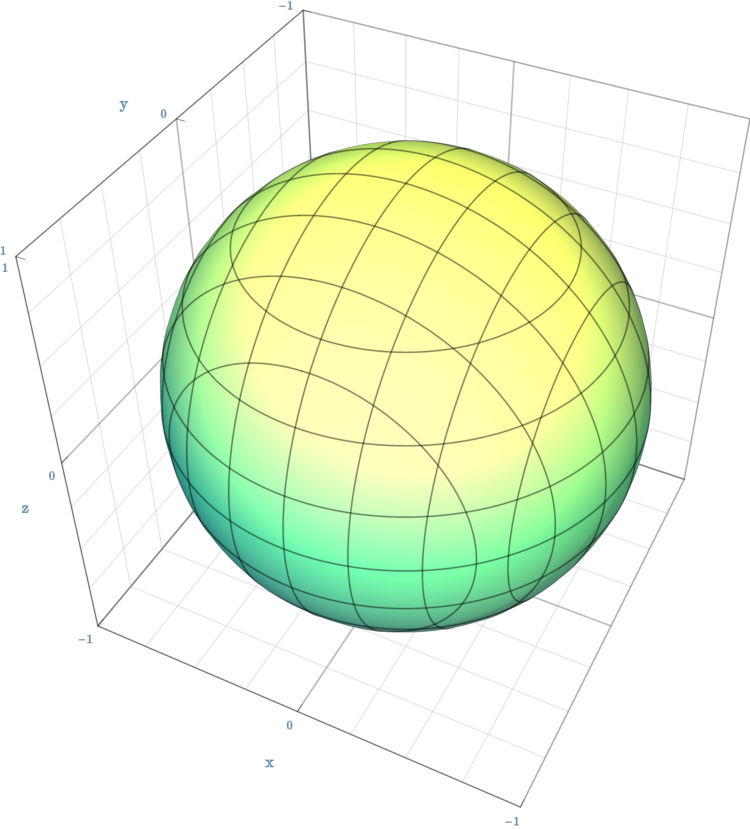

| 圆抛物面 | ${x^{2} \over a^{2}}+{y^{2} \over a^{2}}-z=0\,$ |  |

| 单叶双曲面 | ${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=1\,}$ |  |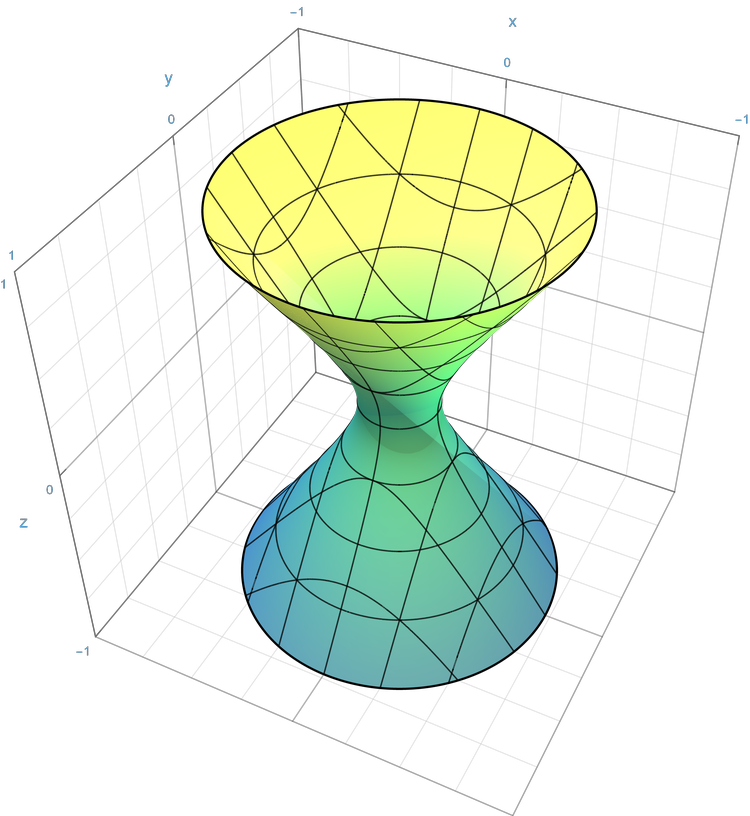

| 双叶双曲面 | ${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=-1\,}$ |  |

| 退化的一般实二次曲面 | 表达式 | 图像 |

| :-: | :-: | :-: |

| 椭圆锥面 | ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0\,$ |  |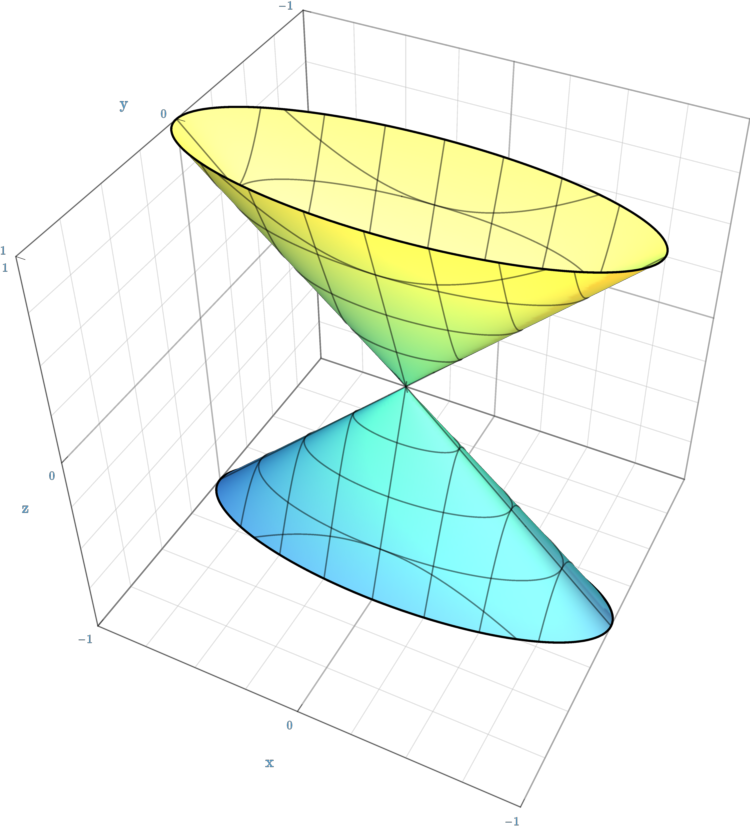

| 锥面 | ${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=0\,}$ |  |

| 椭圆柱面 | ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\,$ |  |

| 圆柱面 | ${x^{2} \over a^{2}}+{y^{2} \over a^{2}}=1\,$ |  |

| 双曲柱面 | ${x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1\,$ |  |

| 抛物柱面 | $x^{2}+2ay=0\,$ |  |

> 简约版:

>

> - 缺一变量变量且有平方和表示一个母线平行于 z 轴的柱面

> - 变量 z 为负数的图像两头大中间小

> - 变量 z 分之斜率的图像是锥面

## 直线的表达式

- 第一类: $x=k_0±a, y=k_1±b, z=k_2±c$, 其中 k 为点的坐标, a,b,c 为直线的斜率

- 第二类: $\frac{x±k_0}{a}=\frac{y±k_1}{b}=\frac{z±k_2}{c}$, 其中 k 为点的坐标, a,b,c 为直线的斜率

## 渐近线

- 曲线的水平渐近线: y = $\lim_{x\to\infin}f(x)$

- 曲线的垂直渐近线: $\lim_{x\to无意义点}f(x)=\infin$, x = 无意义点

## 向量

- $\overrightarrow{a}=1i+1j+1k$

## 模长

- $|\overrightarrow{u}|=\sqrt{A^2+B^2+C^2}$

- 一个题: 向量 a, b 的模长 |a|=2, |b|=3, 求 |a-b|

> 解: $|a-b|=\sqrt{|a-b|^2} = \sqrt{|a|^2+|b|^2-2 a \cdot b} =\sqrt{13-2 |a||b|cos<a,b>} =\sqrt{13-6} =\sqrt{7}$

## 方向余弦

- ${\{\cos\alpha,\cos\beta,\cos\gamma=\frac{i}{模长},\frac{j}{模长},\frac{k}{模长}\}}$

## 方向角

- 就是方向余弦的值的角度, $\cos\alpha=w, \alpha=$ 方向角

- 可以作为向量的一组: $\frac{\pi}{大}\frac{\pi}{小}\frac{\pi}{小}$

## 法向量

### 法向量定义

- 系数

### 方向向量

#### 方向向量定义

- 直线分母

### 计算与公式

- 求互相垂直直线, 设 $w=\frac{f(x)}{a}=\frac{g(y)}{b}=\frac{Q(z)}{c}$, 用向量 $s= w-所过点_{xyz},s_{所求}\times s_L=0$, 求出 t 代会列的向量求出分母, 分子就是 xyz-过的点

- 法向量差积

> $\overrightarrow{S}=\overrightarrow{n_1}\times\overrightarrow{n_2}=\begin{vmatrix} i & i & k \\ n_1系数_1 & n_1系数_2 & n_1系数_3 \\ n_2系数_1 & n_2系数_2 & n_2系数_3 \end{vmatrix}\\=去掉第一行第一列-去掉第二行第二列+去掉第三行第三列=\begin{vmatrix}n_1系数_2&n_1系数_3\\n_2系数_2&n_2系数_3\end{vmatrix}i-类推j+类推k=交叉相乘再相减i-类推j+类推k$

- 向量垂直

> 向量点乘=0

- 向量平行

>

> - 平行的原向量点分之模长: $\frac{点}{模}$, 模 $=\sqrt{点^2+点^2+点^2}$

> - 平行的单位向量: $±(\frac{点}{模}\frac{点}{模}\frac{点}{模})$

>

- 切线方程

> 两线相交一点, 求切线方程

>

> > 求交点后, 求所求函数切线的斜率, 即一阶导带入交点

> >

> > > 斜率和交点带入切线方程公式 0=k(X-x) - (Y-y) 求得.

> > >

> > > > $k=\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}$

- 法线方程

> 0=w(X-x) - (Y-y), 其中 wk=-1 (k 是切线方程的斜率)

>

> > $w=\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}$

- 点向式方程

> $$

- 直线方程

> 求出方向向量, 找出经过的点, 带入点向式方程

### 其他型月世界常见的图形题

- 直线 balabala 与平面平行

> 即平面法向量与直线方向向量垂直

- 平行于一个向量的单位向量

> 平行的向量除以目标向量的模长得到通向的单位向量, 此时再加上负号得到反向的单位向量

- 求曲线 $x=e^t\cos t,y=e^t\sin t$, 在 $t=\frac{\pi}{2}$ 处的法线方程

> 设法线的斜率为 w, 曲线切线的斜率为 k,则 $w=-k\\k=\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{e^t\sin t+e^t\cos t}{e^t\cos t-e^t\sin t}=-1$, 即 $w=1\\$ 当 $t=\frac{\pi}{2}$ 时, $x=0, y=e^\frac{\pi}{2}\\$ 此时法线方程为 $(y-e^\frac{pi}{2})=(x-0), 即y=x+e^\frac{\pi}{2}$

- 两曲线的切线互相垂直: 一阶导相乘=-1

# 应用题

- 圈地求极值型

> 列出方程, 1 次导数得值, 二次导数证明极值

## 物理应用

- 牛顿第二定律

> 物体质量 m, 物体加速度 a, 物体动能 F=ma

>

> > 加速度 $a=\frac{d^2x}{dt^2}=\frac{dv}{dt}=v\frac{dv}{dt}$, 分离变量可以积分

> >

> > > 正比 F=kt, 反比 Ft=k, 一正一反 Fv=kt

> > >

> > > > 若有积分求得 balabala+C, 还要带入条件求出 C 的具体值, 然后再带入求得的积分成为函数式

- 变化率问题

> 形如有总数 N, t 时刻某量 y 对 t 的变化率与 t 时刻某量 x 成正比: $y(x)=\frac{dx}{dt}=±kx(N-x)$

>

> > 注意标注变化率的正负

- 冷却定律 (高概率考题)

> t 时刻 T(t)的时间对温度的变化率与 t 时刻物体与介质的温差 $T-T_0 成正比$

>

> > > $\frac{dT}{dt}=-k(T-T_0),\frac{dT}{dt}<0$

> > >

> > > > 会出现一阶线性常微分方程, 时间 t 为变量 x, 解如 $W=Ce^{-\int kdt}+W_0$, 其中原式形如 $\frac{dW}{dt}=±k(W-W_0)$

# 证明题

## 中值定理系

### 拉日型

- 常见于问两个点使 balabala 成立

> 首先作辅助函数 (我也不知道怎么做. 大概和画辅助线一样属于和出题人思路碰一碰) 然后画数轴, 设一点分割另外两点, 分类讨论一下

### 拉日型例题

- 已知函数 f(x)在[0,1]上连续,在(0,1)内可导,且 f(0)=0,f(1)=1, 试证明:\\(1)存在 $\xi\in(0,1)$ 使 $f(\xi)=1-\xi\\(2)$ 存在两个不同的点 $\eta,\mu\in(0,1)$ 使 $f`(\eta)f`(\mu)=1$

> (1)设辅助函数 $F(\xi)=f(\xi)-1+\xi\rightarrow F(x)=f(x)-1+x, x\in(0,1)$

>

> > $F(0)=f(0)-1+0=-1<0, F(1)=f(1)-1+1=1>0$, 由零点定理可得必有一点 $\xi$ 使 $F(\xi)=0$, 即 $f(\xi)=1-\xi$

>

> (2)设一点 $\xi,\eta\in(0,\xi),\mu\in(\xi,1)\\∵f(x)$ 在 $[0,1]$ 上连续,在(0,1)内可导, ∴f(x) 在 $[0,\xi]$ 上连续,在 $(0,\xi)$ 内可导,$[\xi,1]$ 上连续,在 $(\xi,1)$ 内可导 由拉日定理得 $f`(\eta)=\frac{f(\xi)-f(0)}{\xi-0},f`(\mu)=\frac{f(1)-\xi}{1-\xi}$ ,联立 $f(\xi)=1-\xi$ 得 $f`(\eta)f`(\mu)=\frac{1-1+\xi}{\xi}=1$ ,证毕

# 错题记录

- $已知f(x)=1-\frac{1}{x}, 则f(f(x))=1-\frac{1}{\frac{1}{1-x}}=1-$ 分子分母同乘 x 然后化简 $=\frac{1}{1-x}$ 化简题吃屎去吧

- $极限\lim_{x\to\infin}\frac{1-2x-x^2}{x^2}=$

> $\frac{1}{x^2}-\frac{2x}{x^2}-\frac{x^2}{x^2}=\frac{1}{x^2}-\frac{2}{x}-1=带入无穷=0-0-1=-1$ 化简题吃屎去吧

- $当x\to{0}时2-2\cos{x}~ax^2=$

> $\lim_{x\to{0}}\frac{2-2\cos{x}}{ax^2}=1,其中1-\cos{x}=\frac{x}{2}$, 带入然后解得 a=1

- 函数 $f(x)=1-|x-1|$ 在点 x=1 处连续但不可导, ∵ 左极限 ≠ 右极限

- 若曲线 $f(x)=1-x^3$ 与曲线 $g(x)=\ln{x}$ 在自变量 $x=x_0$ 时的切线相互垂直, 则 $x_0$

> $x_0=f`(x_0)g(`x_0)=-3x^2×\frac{1}{x}=0, x_0=\frac{1}{3}$

- 设函数 f(x)在区间(-1,1)内连续, 若 $x\in(-1,0)$ 时, $f`(x)<0;x\in(0,1)$ 时, f`(x)>0,则在区间(-1,1)内:

> f(0)是函数的极小值 (极值第一判定)

- 向量 a=j+k 的方向角是啥?

> $\frac{\pi}{2},\frac{\pi}{4},\frac{\pi}{4}$ 小编也不知道

- 已知 $e^{-x}$ 是微分方程 $y``+3ay`+2y=0$ 的一个解, 则 a=?.

> 令 $y=e^x,y`=-e^{-x},y``=e^x$, 带入原式得 $e^x-3ae^{-x}+2e^x=0, 即1-3a+2=0, a=1$

- $\int\int_{区间D}f(x,y)dw=\int_0^1\:dx\int_0^x\:f(x,y)dy$ 变换积分次序:

> 交换区间, $0≤x≤1, 0≤y≤x$ 可以换为 $y≤x≤1,0≤y≤1$, 则交换后的积分次序为 $\int_0^1\:dy\int_y^1\:f(x,y)dx$

- 函数 $f(x)=e^{1-x}$ 在点 x=0.99 处的近似值

> magik 变换之 $x=1,\Delta{x}=-0.01, f(0.99)=f(x+\Delta{x})=f(x)+\Delta{x}f`(x)=e^{1-1}+(-0.01)(-e^{1-1})=1+0.01$

## 我最喜欢的脱裤子放屁题

- 用钢板做成一个表面积为 54 平方米的有盖长方体水箱, 欲使水箱的容积最大, 则水箱的最大容积为?

- 设 $D=\{(x,y)|1≤x^2+y^2≤4,x≥0,y≥0\}$ 则二重积分 $\int\int_{D}4dxdy=?$